Storing trees in a database table

Published: 25 Dec 2021
Written by: Chun Fei Lung

Relational databases are very good at storing tabular data, but what if you need to store arbitrarily-sized trees?

I mean, technically it fits

Many things can be modelled as a tree. Organisational hierarchies for example, or directory structures, or geographical divisions like this one:

World
└ North America
  └ United States
    └ California
      └ Berkeley
      └ Pasadena
    └ Massachusetts
└ Europe
  └ France
  └ United Kingdom
    └ England
      └ London
    └ Scotland
    └ Wales
    └ Northern Ireland

Trees aren’t very complicated data structures. We can easily whip up a Location class that is able to represent both a tree and its elements:

class Location
{
    private string $name;
    private ?Location $parent = null;
    private array $children = [];

    public function __construct(string $name)
    {
        $this->name = $name;
    }

    public function addChild(Location $location): void
    {
        $this->children[] = $location;
        $location->setParent($this);
    }

    // Stupid getters and setters go here
}

The following code snippets shows how we can use this Location class to create an instance that contains the entire tree from the example above:

$world = new Location('World');
$world->addChild($northAmerica = new Location('North America'));

$northAmerica->addChild($unitedStates = new Location('United States'));

$unitedStates->addChild($california = new Location('California'));
$unitedStates->addChild(new Location('Massachusetts'));

$california->addChild(new Location('Berkeley'));
$california->addChild(new Location('Pasadena'));

$world->addChild($europe = new Location('Europe'));

// ...
//
// You get the idea

This is nice and all, but it would be even nicer if we could also store the contents of $world somewhere.

There are several NoSQL databases that are made specifically to store and query data structures like trees, but sometimes all you have – or want – is a relational database. Maybe you don’t want to maintain a separate NoSQL database. Or maybe you are bound to an ORM framework that only supports relational databases, like MySQL and SQLite.

Fortunately it’s totally possible to store trees in a relational database!

A simple solution

We could simply convert the Location class into an ORM-managed entity that looks roughly like this:

location
id	name	parent_id	order
1	World		0
2	North America	1	0
3	United States	2	0
4	California	3	0
5	Berkeley	4	0
6	Pasadena	4	1
7	Massachusetts	2	1
8	Europe	1	1
9	France	8	0
10	United Kingdom	8	1
11	England	10	0
12	London	11	0
13	Scotland	10	1
14	Wales	10	2
15	Northern Ireland	10	3

Each record stores a single Location. With the exception of the root node, each Location stores a reference to its parent (parent_id) and its position in $children (order). This table contains all the information we need to recreate the original tree.

While this solution is intuitive, it suffers from several issues:

Almost each row contains a foreign key reference to a different row. This is a pretty minor issue, but it does mean that storing trees can be somewhat cumbersome.
Trees can only be retrieved recursively. This makes sense, because our Location class is also implemented as a recursive data structure. However, it often means that you need to execute multiple individual queries to retrieve the entire tree. Common table expressions (CTEs) allow you to execute recursive queries, but I haven’t encountered many ORM frameworks yet that support them natively.

Nested sets

There is another method to store trees in a relational database, without the need for foreign keys and recursive queries. The nested set model works by traversing the tree in a systematic way and assigning an incrementing number to each node that it enters or leaves.

The figure below shows what this looks like for the tree that I showed at the beginning of the article:

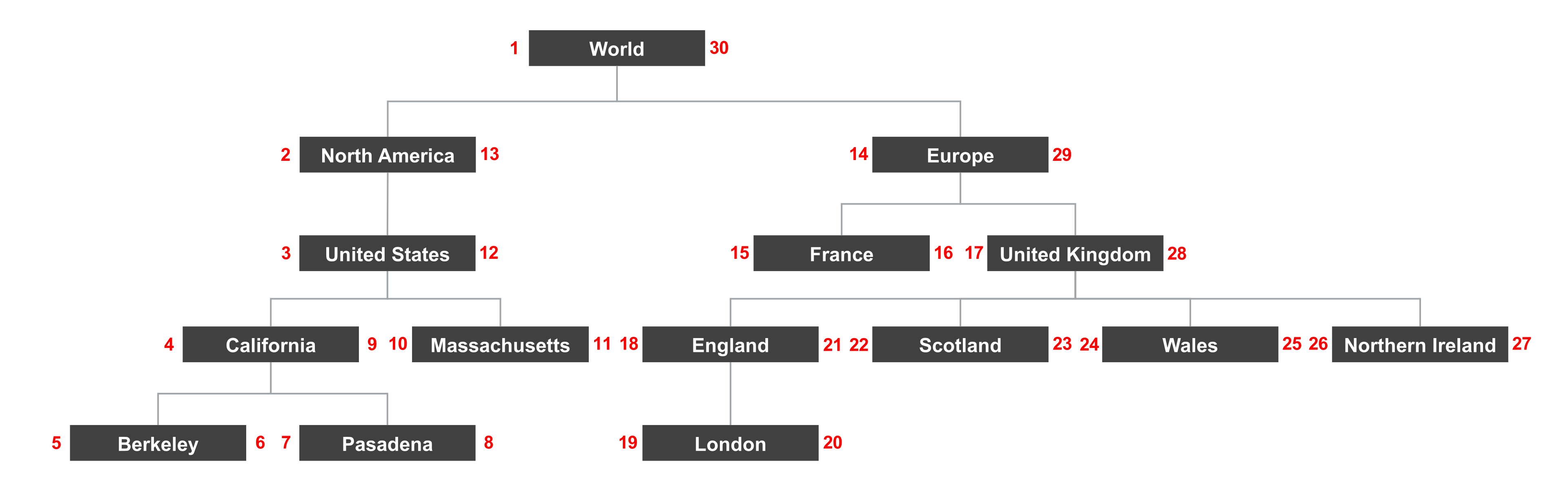
Result of applying a nested set algorithm to the example tree

The traversal starts at the root node (“World”) and then tries to visit the first child of every node that it can find. Once it encounters a leaf node (“Berkeley”) it tries to move to a sibling (“Pasadena”) or its parent’s sibling (“Massachusetts”). This process is repeated until it finally reaches the root node again.

After computing the “left” and “right” values for each node in a tree, we can simply store these values in a table:

location
id	name	left	right
1	World	1	30
2	North America	2	13
3	United States	3	12
4	California	4	9
5	Berkeley	5	6
6	Pasadena	7	8
7	Massachusetts	10	11
8	Europe	14	29
9	France	15	16
10	United Kingdom	17	28
11	England	18	21
12	London	19	20
13	Scotland	22	23
14	Wales	24	25
15	Northern Ireland	26	27

Note that this representation has a few interesting (albeit not always very useful) properties:

The left value of the root node is always equal to 1, while its right is always double the number of nodes in the tree.
The difference between the left and right values for a node tells you something about how large its subtree is. The smallest nodes (leaves) have no children, which always results in a difference of 1.
Each descendant of a node n has a left value that is greater than that of n and a right value that is less than that n. This means that we can simply retrieve the entire “North America” subtree by retrieving all Locations with left >= 2 AND right <= 13.

Unfortunately, this representation also suffers from a few minor issues.

The most notable issue with this representation is that it is not as intuitive as the simple solution that I described above. This should be a one-time problem however: once you have implemented the logic for the nested set model, there is no need to think about it ever again!

Another issue is that this representation makes it harder to figure out a node’s direct descendants (i.e. its children). We can easily fix this by adding another field that stores the level (or depth) of the node, so that you can add a WHERE child.level = node.level + 1 to your queries:

location
id	name	left	right	level
1	World	1	30	0
2	North America	2	13	1
3	United States	3	12	2
4	California	4	9	3
5	Berkeley	5	6	4
6	Pasadena	7	8	4
7	Massachusetts	10	11	3
8	Europe	14	29	1
9	France	15	16	2
10	United Kingdom	17	28	2
11	England	18	21	3
12	London	19	20	4
13	Scotland	22	23	3
14	Wales	24	25	3
15	Northern Ireland	26	27	3

Storing trees in a database table

A simple solution

Nested sets

More about databases

More about programming