Scalable transfer patterns
Route planning is largely a solved problem. Route planning for public transport networks can still be challenging however, especially if it those networks need to cover the entire world. This week’s paper gives you some insight into the steps that are needed to make it work (preferably before the heat death of the universe).
At first glance, journey planning for public transport seems like a normal pathfinding problem. In a way, that’s true: one can simply use Dijkstra’s algorithm (or some variation thereof) to find an optimal route.
But journey planning in public transport networks poses some additional challenges:
-
Buses and trains often depart at fixed times, i.e. a route that’s viable now might not be available any more in an hour;
-
The shortest route is not necessarily the best route – there are many other criteria that must be considered, e.g. travel time, number of transfers, and ticket prices;
-
Transfers are an important part of journeys in public transport, but are hard to model realistically;
-
Networks are prone to delays and other types of real-time changes which may make some routes infeasible;
-
Pathfinding algorithms for public transport networks often require preprocessing steps that cost a lot of time and space.
Existing approaches work reasonably well when applied to metropolitan areas, but are hard to scale to networks that cover whole continents .
The paper describes a more efficient method to preprocess transfer patterns for a public transit network.
Let’s look at the “old” approach to transfer patterns first, so we can understand what makes the new one better.
Transfer patterns
Journeys in a public transport network are time-dependent, which greatly increases the size of the network in which we need to find our optimal route. The network itself isn’t as time-dependent though, as it’s simple and static enough to print on physical maps.
The basic idea behind transfer patterns therefore is to find optimal routes through the network without considering temporal aspects. Each route consists of a sequence of stops at which a traveller transfers to a different vehicle or changes their . These patterns can be efficiently stored in a directed acyclic graph.
However, storing and querying patterns will still become prohibitively expensive very quickly in large, dense networks.
Hubs
Some stops in a network are more important than others, especially in journeys that cover larger distances.
These important stops are called hubs, and are typically part of many optimal routes. You can use them to your advantage by stopping searches from non-hubs for a route as soon as a hub is reached.
Another useful heuristic is to only consider routes with at most two transfers to and from non-hubs, as routes with more transfers are likely to be suboptimal anyway.
This approach leads to another considerable reduction in space consumption. Unfortunately it does little for preprocessing times, which may still exceed 3,000 hours on a single core for the North American continent.
The authors present some improvements that aim to further reduce the amount of time and space needed to preprocess transfer patterns by exploiting some other key characteristics of public transport networks.
Clustering
You’ll often find that lines in a public transport network are not arranged as if they’re in a bowl of spaghetti, but grouped into clusters that are operated by different transport agencies. There are only few connections between clusters, and the few connections that do exist can typically be found near the boundaries and in long-distance hubs.
If you’re lucky, the data already contains information about who operates each line. In other cases you can usually get similar groupings by applying clustering algorithms to the network:
- k-means clustering can be used to cluster stops based on their geographical coordinates. The downside of this approach is that it ignores the structure of the network and requires the user to specify the number of clusters (k);
- Merge-based clustering is an alternative approach that does take the network structure into account and works by merging network partitions until some upper bound size is reached. This is a little bit better, but still requires the user to specify an upper bound;
- METIS is a general-purpose graph-clustering algorithm. It first creates a coarse (simplified) version of the network that can be easily partitioned. Then it compares the complete graph with the coarse version to assign the remaining parts of the network to clusters.
- PUNCH is an algorithm that was originally developed for road networks. It is similar to METIS, but simplifies networks by shrinking them without changing their “shape”.
Merge-based clustering is probably the most effective way to do this.
Anyway, once a set of clusters has been identified, we can look at long-distance and border stops: these are special stops that allow someone to travel directly to stops from neighbouring clusters and play an important role in determining optimal journeys between clusters.
Some clusters may have a large number of border stops. Having too many of them will make it hard to calculate optimal routes however, so we’ll want to keep that number as low as possible.
The authors therefore conclude the clustering phase with a post-processing step in which clusters are merged if the resulting cluster would have dramatically fewer border stops.
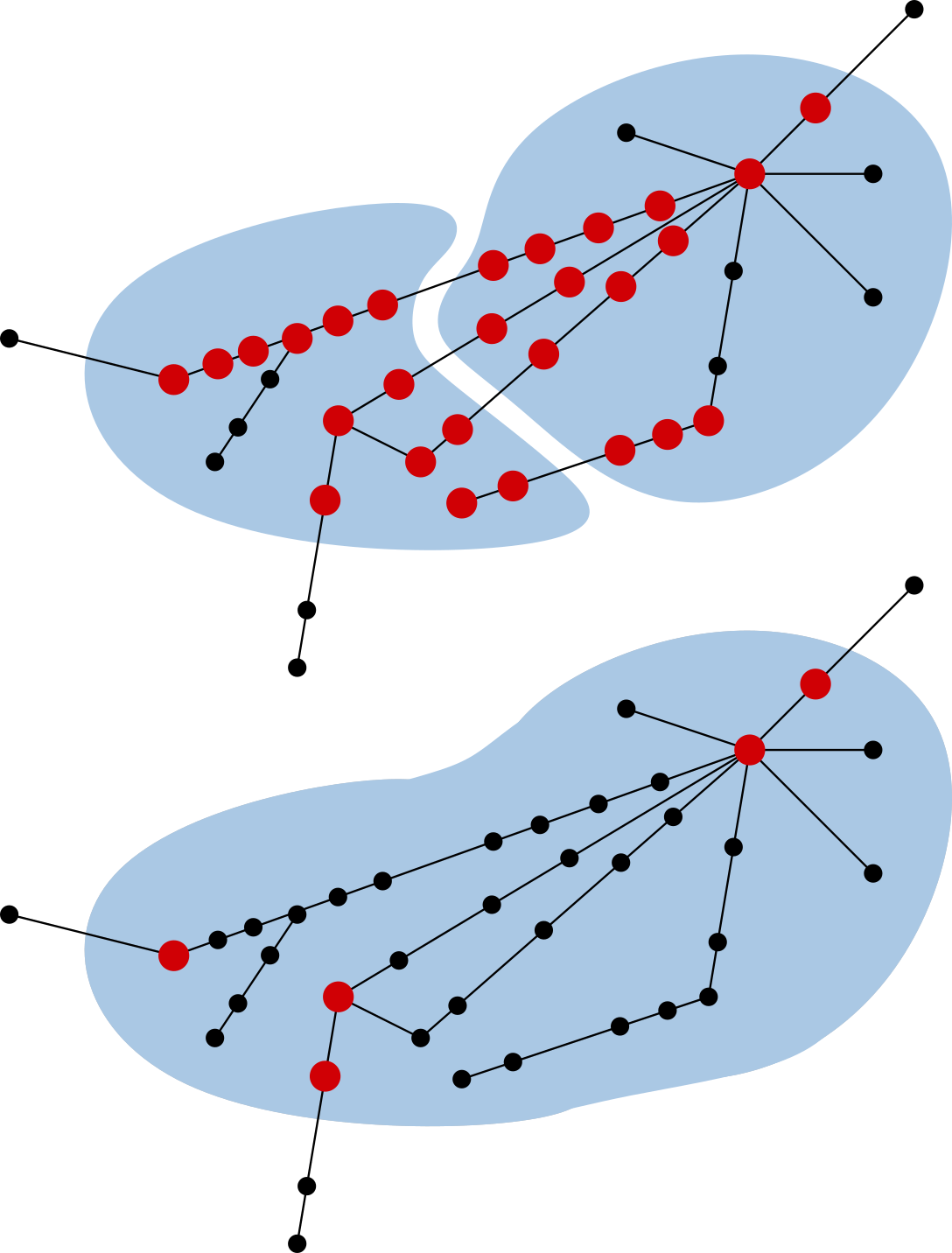
If two neighbouring clusters have a large number of border stops (red), merging can be an easy way to get rid of a lot of them.
Routing within clusters
Every cluster should be at most the size of a metropolitan area now.
This is great, because it means we can now use the basic transfer pattern approach for optimal routes within clusters without the need to consider hubs.
Then we also need to be able to compute journeys between clusters. Recall that there are two ways to move from one cluster to another: long-distance stops and border stops.
Long-distance routing
Networks generally don’t have a lot of long-distance stops. This makes it feasible for us to compute optimal routes between all long-distance stops in a network.
Once we have done that, we can efficiently compute approximately optimal routes between any two stops by combining our long-distance transfer patterns with the local transfer patterns from the previous step.
Note that each cluster must have at least one long-distance stop for this to work!
Between clusters
Not all inter-cluster routes need to go through a long-distance stop, especially if they start or end near the edge of a cluster.
We’ve already computed optimal routes within clusters, which includes boundary stops. For journeys between stops from different clusters we therefore only need to find optimal routes between boundary stops.
The authors evaluate the performance of their new approach by comparing it with the existing transfer pattern approach.
This is done by applying both algorithms to Germany’s public transit network and extrapolating the results to a fictitious network that covers the entire world.
There’s also a correctness proof by the way, which I’ve skipped here. You can find it in the original paper.
Overall results of the time and space consumption are displayed in the table below.
| Germany | World | |||
|---|---|---|---|---|
| Time (h) | Space | Time (h) | Space | |
| Scalable transfer patterns: local patterns | 12.5 | 760 MB | 200 | 20 GB |
| Scalable transfer patterns: long-distance patterns | 2.7 | 180 MB | 1,250 | 4 GB |
| Scalable transfer patterns: border patterns | 1.3 | 400 MB | 600 | 10 GB |
| Scalable transfer patterns: total | 16.5 | 1,160 MB | 2,050 | 30 GB |
| Conventional transfer patterns: without hubs | 372.0 | 140 GB | 140,000 | 50 TB |
| Conventional transfer patterns: with hubs | 350.0 | 2 GB | 20,000 | 3 TB |
It’s clear that the scalable transfer pattern approach is much cheaper than the conventional approach that was used before 2016 in literally every way.
Query times are pretty impressive as well, and range from 0.1 ms on a local cluster to 200 ms on non-local queries for the whole world!
-
Optimal routes in a public transport network can be stored efficiently in a directed acyclic graph using transfer patterns
-
Some stops in a network are more important than others and should be treated differently
-
Segmenting a public transport network into clusters makes transfer pattern approaches much more scalable: divide and conquer!
-
A lot of unnecessary computation can be avoided by preprocessing optimal routes in an optimal order


